Cálculo diferencial e problemas de otimização

Matemática

Quando você fala em cálculo diferencial e integral, tem-se um importante mecanismo matemático, que vai além da relação entre variáveis e funções. Pode-se otimizar algo, ou seja, dar-lhe uma configuração que melhore ao máximo seu desempenho, ou reduza ao mínimo o consumo de material para produzi-lo.

» A derivada direcional

» Tipos de descontinuidades

» Continuidade de funções

Para resolver um problema de otimização:

1. Deve-se compreender o problema e extrair dados e incógnitas.

2. Após, deve-se tentar visualizar, o que pode ocorrer por meio de um esboço ou desenho.

3. Deve-se estabelecer algumas variáveis para descrever as unidades de interesse e independentes.

4. Essas unidades devem ser organizadas, se possível, na forma de uma função. E, melhor ainda se puder colocar uma única variável dependente de interesse.

5. Depois trabalhamos princípios de derivação, intervalos e outros, levando aos valores otimizados do problema.

Vamos a um exemplo para poder entender melhor.

1. Queremos um retângulo com perímetro 24 cm e com a maior área possível.

Poderíamos começar a chutar respostas ao problema, mas isso seria inadequado, pois podemos chegar a um resultado, mas não o ótimo. Ou chegar a ele e não ter como provar.

Então vamos tentar pensar a respeito do problema. Se a área A a ser otimizada é composta por um retângulo de lados x e y, a área A = xy e o perímetro P = 2(x + y).

Nós temos o valor do perímetro. Com isso, conseguiremos reduzir a uma expressão de função de uma variável.

24 = 2(x + y)

12 = x + y

y = 12 - x

A = xy = 12x – x²

A função A(x) é que deve ser otimizada. Para isso, precisa-se definir os máximos e mínimos da função em seu domínio. A variável x pode oscilar de 0 a 12, ou seja, esse é o domínio.

Vamos usar o método do intervalo fechado. Além de 0 e 12, precisamos definir os números críticos, que são aqueles onde a derivada é nula, ou seja, onde também existe a possibilidade de máximos e mínimos.

A'(x) = 12 - 2x = 0

A'(x) = 2(6 - x) = 0

x = 6.

Assim, os números críticos são 0, 6 e 12. Aplicando A(x) em cada um deles, temos:

A(0) = 0

A(6) = 36 cm²

A(12) = 0

Os menores valores são mínimos globais e o máximo está em x = 6. Sendo y = 12 - x = 6, chegamos à conclusão que o quadrado de lado seis é o que apresenta a maior área com o perímetro de 24 cm.

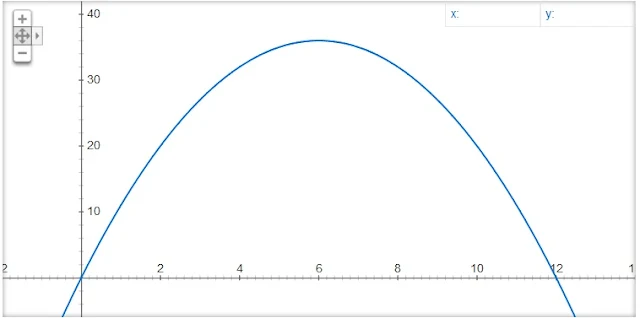[Gráfico de A = 12x - x². Imagem: Gerador de Gráficos do Google]

 

□

👉 E ainda mais para você: A função modular

GOSTOU DESTA POSTAGEM ☺? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS 😉!