Qual o tamanho do infinito?

 Matemática

 

Roberto Carlos, em “Quando digo que te amo”, canta que não sabe o tamanho do infinito, mas é esse o tamanho do seu amor. Nesse embalo poético e musical, os matemáticos também se debruçaram ao longo de suas vidas para entender que tamanho é esse, e ainda chegaram a ideias mais surpreendentes, como a dos infinitos maiores do que outros.

 

[Representação do infinito. Imagem: 463259 / Pixabay]

 

DEPOIS, VOCÊ PODE LER TAMBÉM

» As integrais impróprias

 

» Finitude

 

» Inscrito ou circunscrito?

 

CONTANDO OS ELEMENTOS DE UM CONJUNTO

 

Antes de falarmos de infinito, precisamos imaginar alguma grandeza e sua contagem. O número de estudantes em uma escola de ensino fundamental, ou mesmo a quantidade de vídeos que passam por upload a cada dia, são coisas finitas e que se pode contar. Outras coisas, como conjuntos numéricos diversos (naturais ou inteiros, por exemplo), são infinitas.

 

O número que representa a quantidade de elementos dos conjuntos é chamado de “cardinalidade”. Conjuntos maiores terão maior cardinalidade, e ela será infinita em conjuntos infinitos.

 

CONJUNTOS COM MAIS ELEMENTOS

 

Você certamente já se deparou com essa figurinha quando aprendeu os conjuntos numéricos:

 

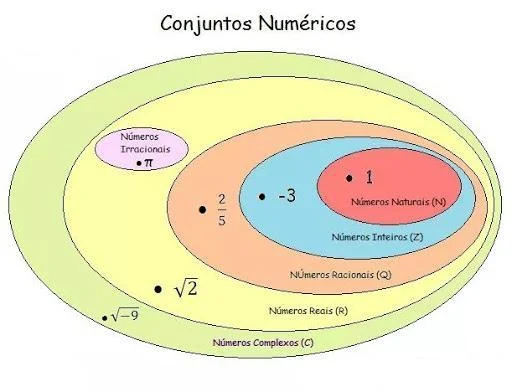[Os conjuntos numéricos. Imagem: Brainly / Reprodução]

 

Sabe-se que o conjunto dos números naturais é infinito. Ao mesmo tempo, também se sabe que para cada natural, exceto zero, existe um inteiro positivo e outro inteiro negativo, ou seja, é um conjunto infinito, mas com o dobro de elementos. Agregando-se novos elementos, novos conjuntos numéricos surgem, com ainda mais elementos.

 

DÍZIMAS NÃO PERIÓDICAS

 

As dízimas não periódicas ou números irracionais, são números cuja parte fracionária não segue um padrão, ou não se tem conhecimento ou recursos computacionais para se afirmar o contrário. Com as dízimas não periódicas, também entendemos outra ideia de qual o tamanho do infinito: aquilo que é tão grande, a ponto de que não saibamos contar e saber a dimensão real.

 

E QUANDO OS LIMITES SÃO INFINITOS?

 

Na definição de Limites, parte importante do Cálculo, os infinitos possuem outras características, como a formação de assíntotas. Na sugestão de post da linha azul 👇🏻, você entende mais do que estamos falando:

 

 

□

 

E AINDA MAIS PARA VOCÊ:

👉 Limites infinitos

 

 

GOSTOU DESTA POSTAGEM ☺? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS 😉!