Anamorfose linear ou linearização de funções

Matemática

O uso da regressão linear ou descrição de um fenômeno por meio de uma reta (função linear), usando pontos experimentais como parâmetro, é importante para a resolução de vários fenômenos. Porém, há casos não lineares em que não seria possível usar uma reta para descrever o fenômeno, usando os pontos experimentais diretamente. Então, uma estratégia é o uso da anamorfose linear ou linearização de funções, que consiste em usar os valores de pontos experimentais 'transformados' por alguma função, e usar estes valores 'transformados' por outra função como 'X' e 'Y' de um modelo linear. Abaixo, apresentaremos alguns tipos de anamorfoses:

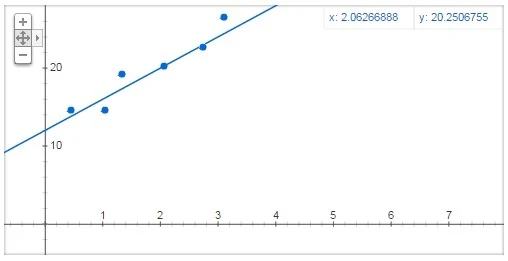[Exemplo de distribuição linear de pontos. Imagem:  Gerador de Gráficos do Google]

» Ajuste por mínimos quadrados para funções polinomiais

» Ajuste por mínimos quadrados para funções lineares

» Resolução de equações biquadradas

Função Exponencial: Na forma Y = AB^X , tomando o logaritmo natural de ambos os membros, temos ln (Y) = ln (A) + X ln (B). Chamando de a o termo ln (A), y = ln (Y) e de b o termo ln (B), chega-se a y = a + bX;

Função Potência: Na forma Y = AX^B , tomando o logaritmo natural de ambos os membros, temos ln (Y) = ln (A) + B ln (X). Chamando de a o termo ln (A), y = ln (Y) e de x o termo ln (X), chega-se a y = a + Bx;

Função Logarítmica: Na forma e^Y = e^AX^B , tomando o logaritmo natural de ambos os membros, temos Y = A + B ln (X). Chamando de x o termo ln (X), chega-se a Y = A + Bx;

Função Hipérbole: Na forma Y = A + B/X. Chamando de x o termo 1/X, chega-se a Y = A + Bx;

Função Hipérbole na Imagem: Na forma Y = 1/(A + BX). Invertendo ambos os membros da equação, temos que 1/Y = A + BX. Tomando 1/Y = y, chegamos a y = A + BX.

Há muitas outras formas de anamorfoses possíveis, incluindo a transformação de raiz quadrada, função hipérbole potência (Y = A/X^B), resolução de equações biquadradas (uma das formas mais comuns), entre outras. É importante dizer que, exceto com modelos matemáticos (modelo exato onde ponto pertence sempre à curva), quando usarmos a anamorfose linear ou linearização, devemos observar os valores estatísticos R e R² (devendo comparar este último para ter uma ideia de qual modelo de linearização escolher).

□

E ainda mais para você: Fazendo regressões lineares usando calculadora científica

GOSTOU DESTA POSTAGEM? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS!