Equações e Inequações no contexto de uma função

Matemática

As equações e inequações, além de apresentarem similaridade em suas resoluções, também possuem uma característica comum: ambas podem ser advindas de uma mesma função. A diferença consiste no significado de cada uma.

[Imagem: O Blog do Mestre]

» Anamorfose linear ou linearização de funções

» Teorema do Sanduíche

» Ajustes por mínimos quadrados para funções lineares

 A equação consiste em uma igualdade, onde se tem incógnitas multiplicadas a coeficientes, cuja soma algébrica resulta no número 0. Pensando-a em termos de uma função y = f(x), a equação corresponde exatamente na intersecção do gráfico de y em função de x com o eixo das abscissas. Em outras palavras, corresponde ao(s) ponto(s) em que se tem y = 0.

Já uma inequação consiste em relação de desigualdade, onde um membro apresenta valor distinto de outro, podendo ser maior ou menor. Pensando novamente em um gráfico de y = f(x), ao fixarmos um valor para y, a inequação será representada por todo o gráfico com y maior e/ou menor do que o valor prefixado.

Podemos tomar como exemplo a equação:

x + 4 = 0

E a inequação

x + 4 > 0

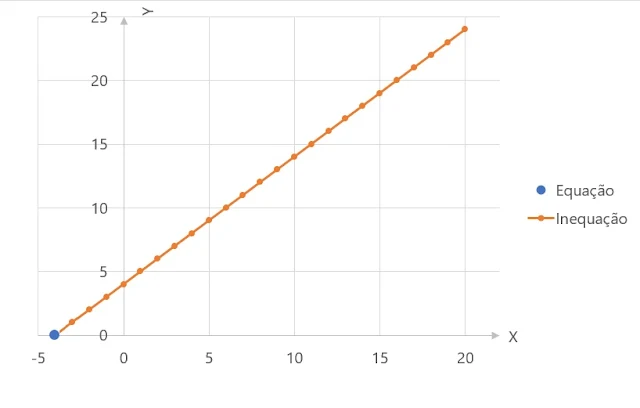
Pensando na função y = x + 4, ilustrada na imagem acima, y assume valor igual a zero apenas de x igual a -4, e, caso x maior do que -4, temos uma inequação. Em nosso exemplo, usamos uma função contínua, com domínio igual aos números reais. Entretanto, caso não houvesse raízes, não haveria equação, apenas inequação, seguindo raciocínio semelhante.

□

E ainda mais para você: Um texto inteiro sobre frações

GOSTOU DESTA POSTAGEM ☺? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS 😉!