Teorema do Sanduíche

Matemática

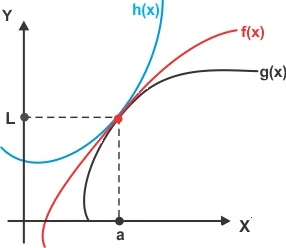
O teorema do sanduíche, espremedura ou confronto, é uma forma de resolver limites de funções que podem não ser tão simples, a princípio, com algum conhecimento do comportamento de outras funções, e a comparação destas com a função da qual se quer saber o limite. A ideia básica é a que está sendo passada pelo nome: achar duas funções que estão ensanduichando a função de que queremos saber o limite em um dado valor a, para um limite quando x tende a a.

[Imagem: Alfaconnection]

» Valores máximos e mínimos

» Derivação Implícita e Logarítmica

» A derivada

Explicitando matematicamente, o teorema do sanduíche nos diz que se g(x) ≤ f(x) ≤ h(x) nas proximidades de a (x tende a a), e se lim _{x →a} g(x) =  lim _{x →a} h(x) = L, então lim _{x →a} f(x) = L. isto é válido para comportamento assintótico, com x tendendo ao infinito.

1) Encontre lim _{x →+∞} (x+1)^½ – (x) ^½

Esta é uma indeterminação da forma ∞ - ∞. Uma forma possível de resolver seria obter a derivada usando a regra de L’Hospital ou usar alguma outra regra matemática cabulosa, como a que vamos usar. Primeiramente, vamos escrever a função g(x) = (x+1)^½ – (x) ^½ de outra forma:

(x+1)^½ – (x) ^½ = (x+1)^½ – (x) ^½ · ((x+1)^½ + (x) ^½)/ ((x+1)^½ + (x) ^½) = 1/((x+1)^½ + (x) ^½)

Agora vem o passo mais importante: escolher quais funções serão os nossos pães: note que g(x) = 0 < f(x) = 1/((x+1)^½ + (x) ^½) < h(x) =1/(2(x) ^½). f(x) < h(x) porque:

 ((x+1)^½ + (x) ^½) > 0 → 1/((x+1)^½ + (x) ^½) > 0

 (x+1)^½ > (x) ^½ → 1/((x+1)^½ + (x) ^½) < 1/((x)^½ + (x) ^½) = 1/(2(x) ^½)

Sabendo que lim _{x →+∞} 0 = 0 e que lim _{x →+∞} 1/(2(x) ^½) = 0, pelo teorema do Sanduíche, é válido afirmar que:

lim _{x →+∞} (x+1)^½ – (x) ^½ = lim _{x →+∞} 1/((x+1)^½ + (x) ^½) = 0.

□

E ainda mais para você: Limites Indeterminados e a Regra de L'Hospital

GOSTOU DESTA POSTAGEM? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS!