Correlação linear entre variáveis

Matemática

Entre duas variáveis qualitativas busca-se verificar a relação por meio de um quadro de contingência e testes de hipóteses como o qui-quadrado. Caso essa relação for apontada por esses mecanismos, dizemos que essas variáveis são associadas (como vimos em outro post, com link sugerido a seguir). E se essas duas variáveis forem quantitativas? Que método podemos usar para verificar a correlação?

[Imagem: UFPR]

» Aproximando a binomial pela normal

» Associação

» Os limites da estimação

DIAGRAMAS DE DISPERSÃO

Para ver correlação, num primeiro momento podemos não ter conhecida uma relação de dependência de uma variável para outra. Mas, ao correr de uma pesquisa científica, a fundamentação teórica poderá ter apontado qual seria a variável independente e qual a variável resposta, que podem ser definidas desde essa etapa.

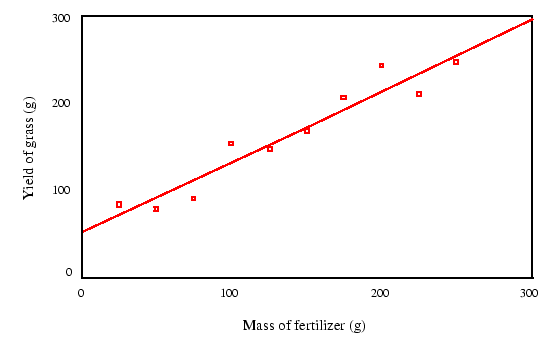
O diagrama de dispersão é um gráfico dos pares ordenados (X,Y) dos pontos experimentais. Com a nuvem de pontos obtidos no experimento sobre um gráfico, é possível observar que tipo de curva pode melhor se ajustar ao fenômeno. Ou, novamente, ver se o formato de curva faz sentido com o que a teoria propõe.

Os formatos mais fáceis de trabalhar são os lineares ou linearizados (que passam por anamorfose linear ou transformação de variáveis, ou ainda por mudança na escala dos eixos ordenados). Mas nem sempre os pontos se ajustam a esses formatos exigindo modelos mais complexos, que podem não permitir uma construção tão fácil, até mesmo manual, do gráfico e da função modelando o fenômeno.

COEFICIENTE DE CORRELAÇÃO DE PEARSON

O coeficiente de correlação de Pearson é uma medida numérica que indica o quão forte pode ser a relação entre duas variáveis quantitativas. Para construí-lo, parte-se do seguinte:

- Padronizar as variáveis, deslocando os eixos coordenados para o centro. Faz-se:

X’ = (X – X_méd)/s_X e

Y’ = (Y – Y_méd)/s_Y

. (variável menos média dividida pelo desvio-padrão amostral).

- Fazer o produto das coordenadas padronizadas dos pontos:

Σ_i=1ⁿ X’Y’

(quando esse somatório dá um valor acima de zero, a correlação linear é positiva, quando abaixo de zero negativa).

- Por fim, fazemos:

r = [Σ_i=1ⁿ X’Y’]/(n – 1)

O coeficiente de correlação de Pearson varia de -1 a 1. Perto dos extremos, temos fortes correlações lineares positivas ou negativas. Perto de 0 já tende a não haver correlação linear.

TESTE DE HIPÓTESES SOBRE COEFICIENTE DE CORRELAÇÃO DE PEARSON

Um critério mais forte para definir correlação linear, em conjunto com o resultado de r, é um teste de hipóteses. Por meio de uma estatística de teste, fornece subsídios para refutar a hipótese nula de não correlação linear.

Calcula-se:

t = [r • (n – 2)]/ (1 – r²)

Com o valor de “t”, observamos a probabilidade de significância (veja mais nos posts sugeridos) associada a esse valor em uma distribuição de probabilidades t de Student com (n – 2) graus de liberdade.

□

👉 E ainda mais para você: Testes de Hipóteses

GOSTOU DESTA POSTAGEM ☺? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS 😉!