Modelo Normal (Curva Gaussiana)

Matemática

Dentro da estatística, há variáveis discretas (domínio contempla números de contagens, por exemplo) ou contínuas. Dentro das contínuas, não se tem probabilidades associadas a valores isolados, mas para conjuntos (intervalos) de valores.

[Imagem: O Blog do Mestre]

» Grandezas direta e inversamente proporcionais e a fórmula da grande reportagem

» Quantas combinações diferentes são possíveis na Mega Sena?

» Amostragem - conceito e diferentes tipos

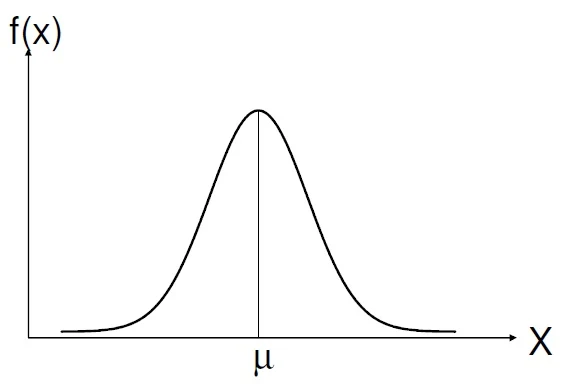
As distribuições de probabilidades em variáveis estatísticas contínuas são definidas por funções f(x) chamadas funções densidade de probabilidade. Elas se caracterizam por, no intervalo de valores da amostra, possuir integral igual a 1.

A curva gaussiana ou modelo normal é representada pela função:

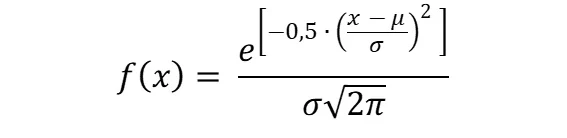[Imagem: O Blog do Mestre]

Onde:

µ = média;

σ = desvio-padrão.

Ela pode modelar muitos fenômenos, sendo amplamente utilizada. É definida de menos a mais infinito, sendo simétrica em torno do eixo central, cujo valor coincide com a média.

Sua forma é chamada de sino, chapéu desabado ou outros nomes. Quão menor a dispersão de dados da amostra (desvio-padrão), mais achatada a curva pode ser.

Caro leitor, note que a fórmula da curva gaussiana é complicadinha e ruim de usar. Podemos facilitar usando a forma padronizada (em função de desvios-padrão).

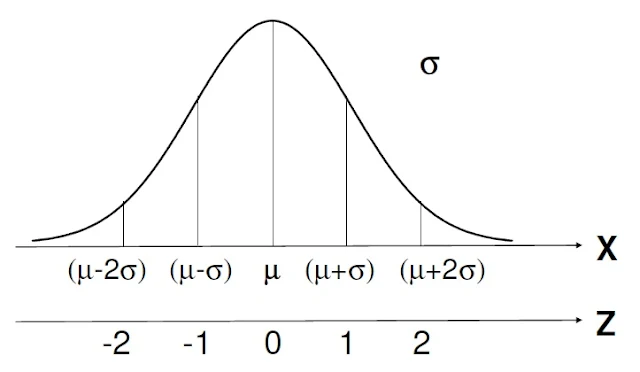
Para cada valor de uma variável X, iremos converter a outra variável Z, cuja relação é de Z = (X - µ)/σ:

[Imagem: O Blog do Mestre]

Com isso, teremos mais facilidade para calcular as áreas sob a curva (probabilidades). A princípio é sabido que as distâncias de um, dois e três desvios-padrão, simetricamente em torno do eixo, levam a áreas (probabilidades) de 68,3 %, 95,4 % e 99,7 %, respectivamente.

Para valores de Z diferentes, podemos usar softwares estatísticos, o Excel, RComander ou ainda tabelas com metade da curva padronizada (para fazer o download de uma, clique aqui).

□

👉 E ainda mais para você: Medidas estatísticas - tendência central e de dispersão

GOSTOU DESTA POSTAGEM ☺? USANDO A BARRA DE BOTÕES, COMPARTILHE COM SEUS AMIGOS 😉!